Derivative Tuning for PID Control
Of the three letters in PID the D, Derivative Tuning, is probably the most misunderstood and certainly the least used! It is well-known that Derivative Tuning is largely unnecessary for fast loops (such as flows and pressures) due to those loops’ naturally quick response time. However, derivative tuning is extremely useful for particularly slow loops (such as temperature) and is an absolute must-have for integrating processes (such as level and insulated temperature loops).
Why is Derivative Tuning Important?
The answer is in the predictive action D provides. When you drive a car and approach a stop sign, you need to apply the brake. But how much brake should you apply? Among other things, the answer depends on how fast you are going and how close you are to the stop sign. The closer you are and the faster you are going, the more brake you need in order to reach the stop sign safely. Applying too much brake or applying it too early means you will not reach the stop sign. Applying too little brake or applying it late means you will travel past the stop sign.
It’s the same in process control. Derivative action is a predictive brake for the controller. We want to use the right amount of D (the brake) so that we get to setpoint quickly (the stop sign) without overshooting (traveling past the goal) or undershooting (stopping short of the goal). And as anyone performing loop tuning can testify, getting the right amount of D is often a difficult task.
To help understand derivative controller action, let’s examine two common misuses of the D term. To aid our study, we’ll examine the effects of the D term on a 3rd order integrating process with a gain rate of 0.34, a deadtime of 40 seconds, a lagtime of approximately 90 seconds, and some higher order dynamics as well. In the following examples, the PID controller uses a non-interacting equation when performing its calculations.
NOTE: Given the integrating nature of this process, PID control in these examples was used with an extremely weak integral term. This essentially created a PD-only tuning situation since the integrating (I) action is naturally built into the process dynamics.
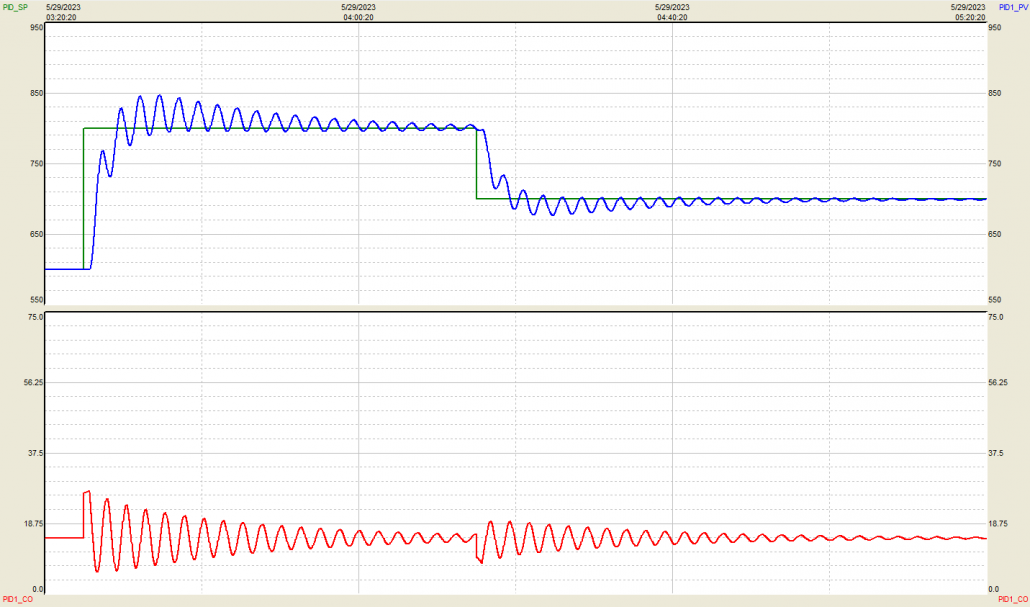
Misuse Example #1: Derivative Tuning Action Too Strong
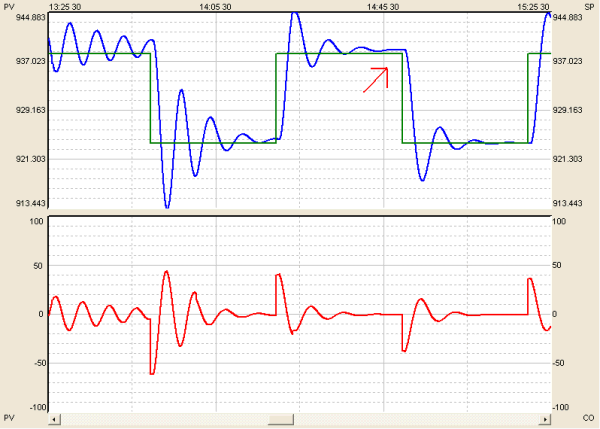
Figure 1 shows the reaction of our process to a PID controller with a Derivative tuning setting that is too strong.
Figure 1. P = 0.6, D = 100. Non-interacting (ISA) equation.
As the trend indicates, so much braking force is applied to the process that our derivative action actually hinders the PV from reaching setpoint. Not only that, but because the derivative action is so aggressive, it is preemptively acting on what it predicts will soon be a negative SP-PV error (though the actual error remains positive). This preemptive action on a predicted negative error is what causes the saw-tooth pattern in the PV and the CO.
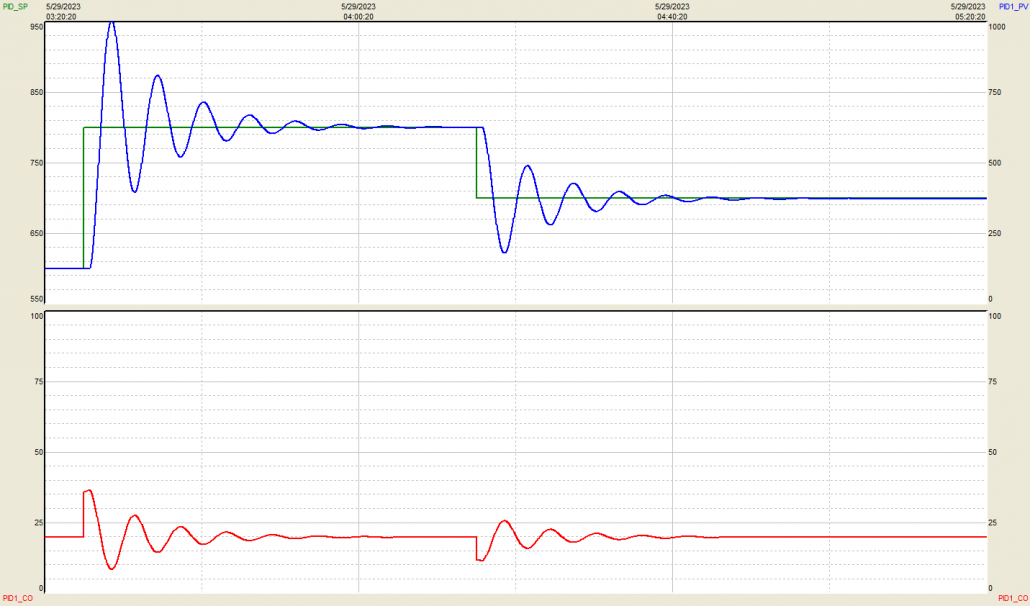
Misuse Example #2: Derivative Tuning Action Too Weak
Figure 2 shows the reaction of our process to a PID controller with a Derivative tuning setting that is too weak.
Figure 2. P = 0.6, D = 5. Non-interacting (ISA) equation.
As the trend indicates, so little brake is applied to the process that our PV far overshoots its goal. For this process, product quality is significantly affected due to poor derivative tuning, and this particular company spends far more on natural gas to heat this loop in startup than is necessary. Multiplied out over similar loops in the rest of the plant, this is a significant energy and product resource waste—all from a poor use of derivative action in PID control.
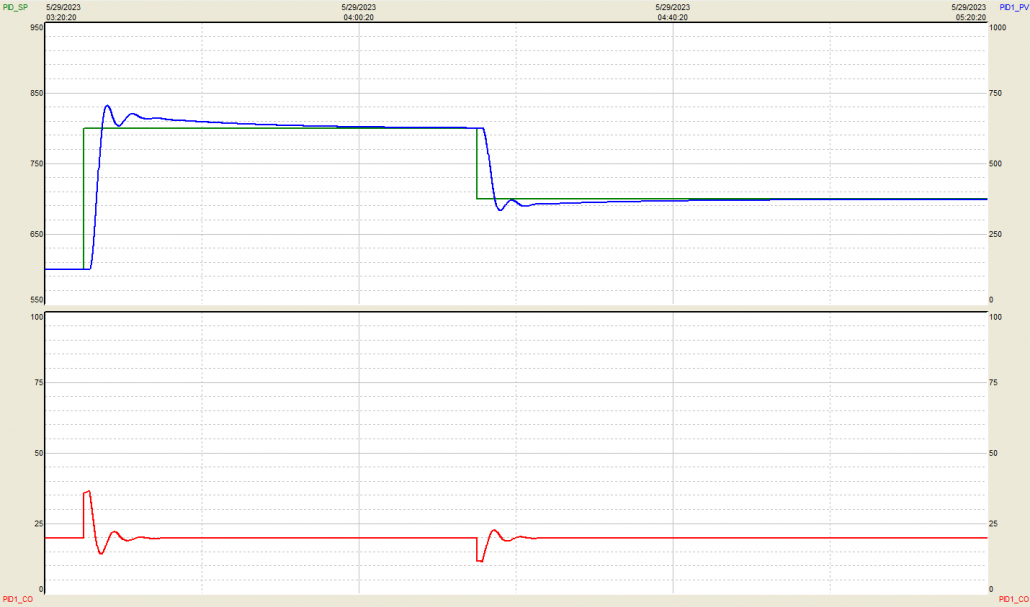
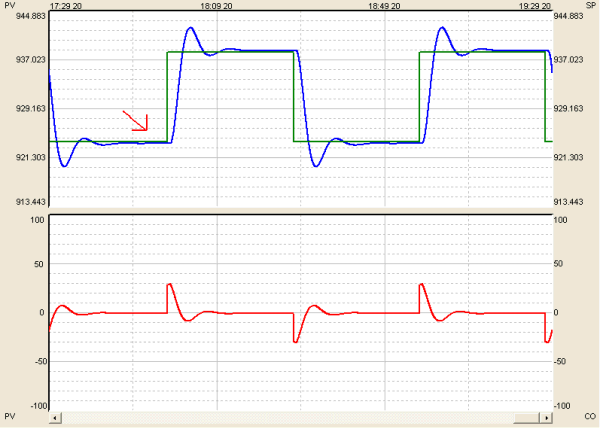
Correct Use Example #3: Derivative Tuning Action Just Right
Figure 3 shows the reaction of our process to a PID controller with a Derivative tuning setting that is just right.
Figure 3. P = 0.6, D = 50. Non-interacting (ISA) equation.
Improving Process Control Performance with PID Loop Tuning Software
In an ideal world, we could easily estimate the right amount of derivative action for a process. Of course, we don’t live in an ideal world and trying to understand the proper amount of D to use can be a long and complicated trial-and-error process, especially if you are tuning slower temperature and level loops.
What if you could have a PID loop professional monitor your process 24 hours a day, 7 days a week and continuously make recommendations about how to adjust your P, I, and D for increasingly better control?
ControlSoft’s Advisory AdaptTune technology, available in INTUNE PID Loop Tuning Tools, provides that exact service.
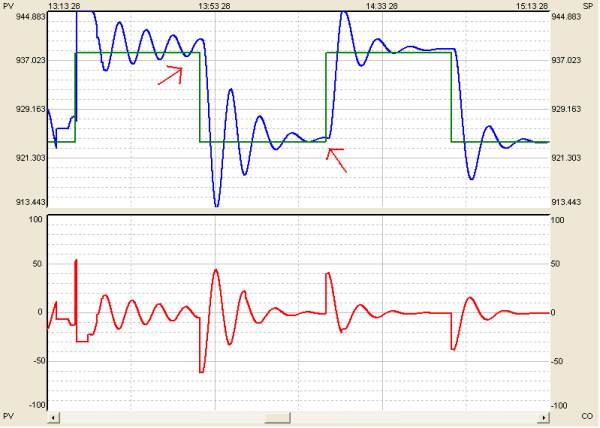
In a recent test, the INTUNE AdaptTune function was allowed to monitor a difficult-to-tune, slow-responding temperature loop that was taking days to tune by hand. Even though it was understood that strong PD control was the proper approach to tuning this loop, the operator could not find the right combination of P and D.
Over the course of just several hours (not days), AdaptTune made several minor recommendations on the P term and several suggested adjustments for the D term to bring the loop under increasingly better control. While in Auto mode, the setpoint was stepped up and down at half-hour intervals to test the response of the new tuning recommendations. The steps were within a healthy operating range for the process.
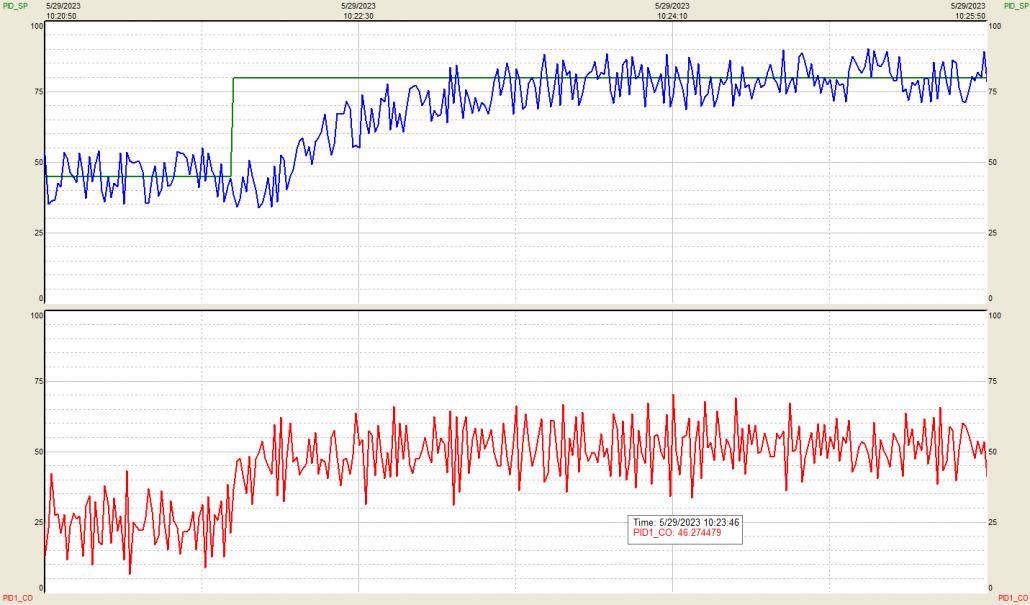
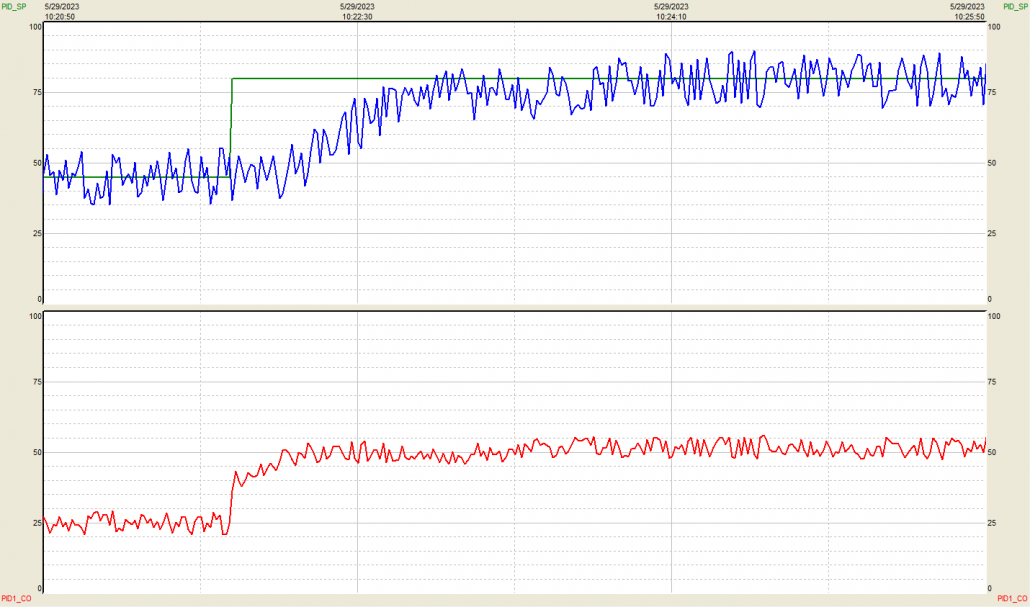
Figure 4. AdaptTune first and second recommendations, indicated by red arrows.
Figure 5. AdaptTune third recommendation, indicated by red arrow.
Figure 6. AdaptTune final recommendation, time indicated by red arrow.
Table 1 shows the recommendations AdaptTune used to bring the loop under control.
Table 1. INTUNE AdaptTune Recommendations.
| Initial | 1st Iteration | 2nd Iteration | 3rd Iteration | 4th Iteration | |
| P | 0.76 | 0.68 | 0.45 | 0.36 | 0.32 |
| I | 3000 | 3000 | 3000 | 3000 | 3000 |
| D | 10 | 12 | 18 | 27 | 33 |
By gradually reducing the Proportional action and strongly increasing the Derivative action, AdaptTune was able to tame one of the operator’s toughest, slowest, and most problematic control loops.
So, Don’t Deny the D. If properly used, derivative control can enhance your controller response for integrating processes and particularly slow loops. Use it with confidence.
Final Word of Caution: Derivative Action Applied to a Noisy Process
As useful as the D term is, and as liberally as it can be applied in the case of slow, integrating processes, Figures 7a and 7b show why it is better to avoid a lot of D if you are dealing with an inherently noisy process.
Figure 7a. Response of PV to a noisy process with D term included in the tuning.
Figure 7b. Response of PV to a noisy process without D term included in the tuning.
To help alleviate this problem, a maintenance team should check the sensors, valves, and other hardware to make sure you are receiving the clearest, most accurate information possible.
You also want to make sure that what appears to be noise is not really a disturbance issue coming from some other aspect of the process upstream.
[This article was first published in 2007 and has been revised for comprehensiveness.]